剑指 Offer 11. 旋转数组的最小数字
一、题目描述
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如,数组[3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转,该数组的最小值为 1。
示例 1:
输入:[3,4,5,1,2]
输出:1
示例 2:
输入:[2,2,2,0,1]
输出:0
二、题目解析
首先,我们明确知道这个数组是被旋转了,也就意味着,这个数组实际上可以被划分为两个部分。
- 1、左边是一个递增的数组
- 2、右边是一个递增的数组
- 3、左右两部分相交的位置出现了一个异常点,小的数字在大的数字后面,比如下图中 1 在 7 的后面,正常来说递增数组应该是 1 在 7 的前面,而在这个位置产生了异常。
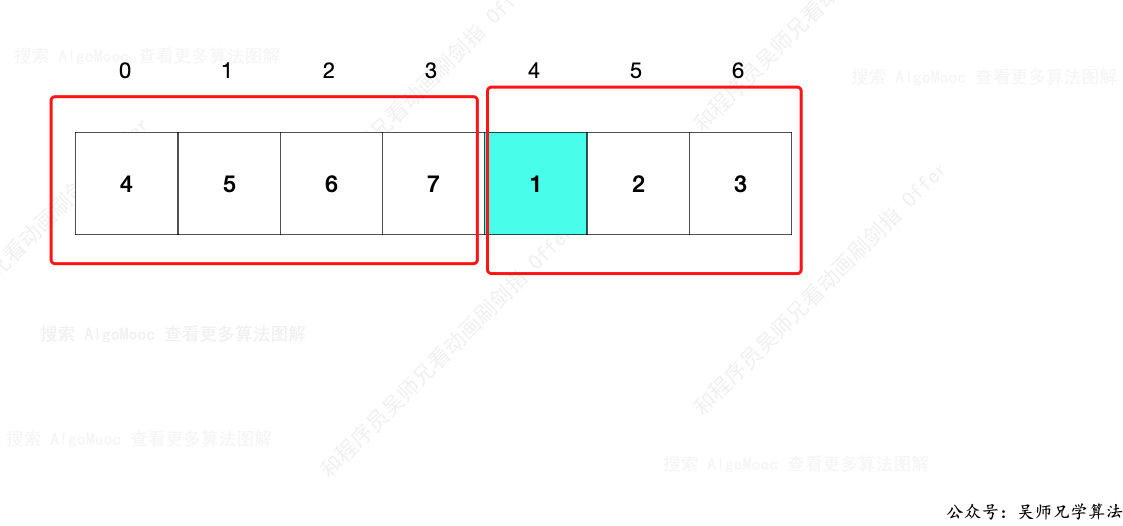
那么,只要我们可以找到异常点,也就找到了旋转数组的最小元素。
具体操作如下:
1、设置两个指针 left 和 right ,其中 left 指向当前区间的开始位置,right 指向当前区间的结束位置,计算出两者的中间索引位置 mid 。
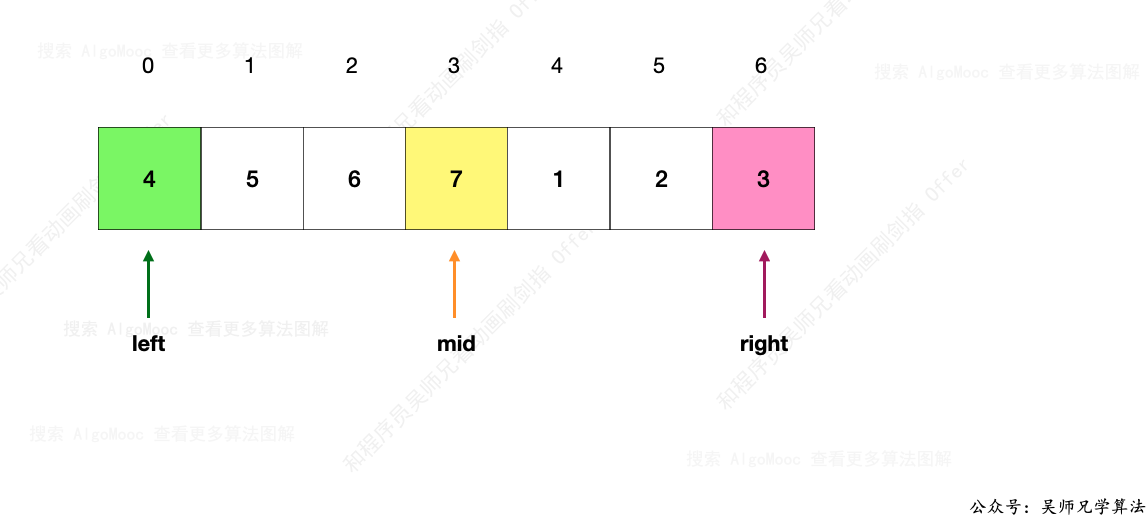
2、接下来,我们研究思考一下这三个指针指向的元素之间的关系。
- 1、如果 mid 指向的元素大于 right 指向的元素,也就意味着异常点肯定是发生在 [ mid + 1 , right ] 这个区间的,不需要再在 [ left ,mid ] 这个区间里面查找,那么可以更新 left 的位置为 mid + 1。
- 2、如果 mid 指向的元素小于 right 指向的元素,也就意味着 [ mid , right ] 这个区间中所有的元素都是正常递增,不需要再在 [ mid , right ] 这个区间里面查找,异常点发生在 [ left , mid ] 这个区间,那么可以更新 right的位置为 mid 。
- 3、由于数组中可能存在重复的元素,比如 [1, 1, 1, 0, 1],那么mid 指向的元素会等于 right 指向的元素,此时无法判断异常点会在哪个区间,因此我们可以从头到尾遍历一下剩下的区间,找到那个最小的元素。
为了帮助你更好的理解整个过程,我特意做了一组动画,点开可以查看:
三、参考代码
// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com
// 作者:程序员吴师兄
class Solution {
public int minArray(int[] numbers) {
// 设置 left, right 指针分别指向 numbers 数组左右两端
// left 指向当前区间的最左边位置,所以初始化为 0
int left = 0;
// right 指向当前区间的最右边位置,所以初始化为 nums.length - 1
int right = numbers.length - 1;
// 循环进行二分查找,直到左端点位置超过了右端点
// 或者在循环过程中找到了起始位置
while (left < right) {
// mid 为中点(这里向下取整,比如 ( 2 + 7 )/ 2 = 4 )
int mid = (left + right) / 2;
// 当 mid 点所在元素大于数组末端的元素时,由于原来的数组是递增有序的,此时出现了异常,大的数在前面
// 所以旋转点在 [ mid + 1, end ] 区间里面
if (numbers[mid] > numbers[right]){
// 所以旋转点在 [ mid + 1, end ] 区间里面 ,更新 left 的位置为 mid + 1
left = mid + 1;
// 当 mid 点所在元素小于数组末端的元素时,由于原来的数组是递增有序的
// 所以旋转点在 [ left, mid ] 区间里面
}else if (numbers[mid] < numbers[right]){
// 旋转点在 [ left, mid ] 区间里面 ,更新 right 的位置为 mid
right = mid;
// 此时,出现了 numbers[mid] = numbers[end] 的情况,无法判断
// [ start , mid ] 为有序数组区间
// 还是 [ mid , end ] 为有序数组区间
// 比如: [1, 0, 1, 1, 1] 和 [1, 1, 1, 0, 1]
}else{
// 所以这里采取遍历的方式
return findMin(numbers,left,right);
}
}
return numbers[left];
}
// 从头到尾遍历 numbers ,获取到最小值
public int findMin(int[] numbers,int left,int right){
// 默认为数组的第一个元素为最小值
int result = numbers[left];
// 从头到尾遍历 numbers
for(int i = left;i <= right;i++){
// 当发现此时遍历的元素值小于 result
if (numbers[i] < result) {
// 那么更新 result
result = numbers[i];
}
}
// 返回 numbers 中的最小值
return result;
}
}




